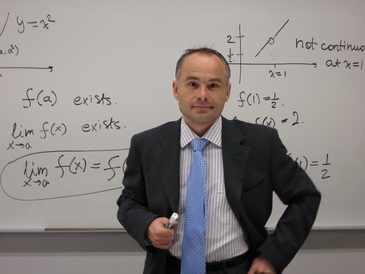Özel Calculus Dersi: Calculus çoğunlukla üniversitelerin 1. sınıflarında öğretilen; integral, türev, fonksiyon, limit, seriler vb. konuları içeren bir derstir.
Calculus, analitik geometri, trigonometri ve cebir konularının üzerine inşa edilmiştir.
Calculus dersi üniversitelerde genelde Calculus I ve Calculus II olarak iki bölümde öğretilmektedir. Bu derslerde başarılı olmak; için temel kavramlara hakim olmak, düzenli çalışmak, çok sayıda problem çözmek ve özel calculus dersi ile mümkündür.
Calculus derslerinin genel olarak kredileri yüksektir. Bu yüzden bu derslerden alacağınız notların akademik ortalamanızın üzerinde büyük bir etkisi olacaktır. özel calculus dersi ile ortalamanızı yükseltin.
özel calculus dersi ile ihtiyacınız olan konulara odaklanarak, aynı dersi defalarca alma zahmetinden kurtulursunuz. özel calculus dersi size başarıya ulaştırıp, üniversitede büyük kolaylık getirir.
özel calculus dersi sonuca götürme odaklı sınavlara hazırlar. özel calculus dersi, ihtiyacınız olan sınav puanları almanıza yardımcı olur.
Üniversitenin ilk yıllarında öğrenciler; genel olarak çalışma düzeni belirlememiş veya bu derslerin önemine hakim olamadıklarından dolayı düşük notlar alarak geçmeyi tercih ediyorlar.
Mezun olduktan sonra akademik kariyer veya diğer alanlarda ortalamaları düşük olduğu için sıkıntı yaşayıp geçmişte bu derslerden aldıkları düşük notlardan pişmanlık duyuyorlar.
Sizde bu pişmanlığı yaşamak istemiyorsanız ve özel calculus dersi ile başarıyla geçmek istiyorsanız bizi arayın.
Eğitim Konuları
- Reel Sayılar ve Reel Doğru
- Doğrular
- Çemberler ve Paraboller
- Fonksiyonlar ve Grafikleri
- Belirli Fonksiyonlar
- Matematik Modeller
- Fonksiyon Kuralları
- Öteleme Kuralları
- Trigonometrik Fonksiyonlar
- Limit ve Süreklilik:
- Değişim Oranı ve Limit
- Limit Bulma, Tanımı ve Kuralları
- Tek Yönlü
- Limitler ve Sonsuzda Limit
- Sonsuz Limit ve Dikey Asimptotlar
- Süreklilik
- Teğet ve Türev.
- Fonk. Olarak Türev ve Kuralları
- Değişim Oranı Olarak Türev
- Trigonometrik
- Fonksiyonların Türevleri
- Zincir Kuralı ve Parametrik Denklemler
- Kapalı Türetme
- Lineerizasyon ve Difransiyeller.
- Türev Uygulamaları:Fonksiyonların Ekstrem Değerleri
- Ortalama Değer Teoremi
- Monotonik
- Fonksiyonlar ve Birinci Mertebe Türev Testi
- Konkavite ve Eğri Çizimi
- Uygulamalı Optimizasyon Problemleri
- Belirsizlik Durumları ve L’Hopital Kuralı
- Newton Metodu ve AntiTürevler
- İntegral:Sonlu Toplam ile Hesaplama
- Sigma Notasyonu ve Sonlu Toplam Limiti
- Belirli İntegral
- Calculus Hesabın Temel Teoremi
- Belirsiz İntegraller ve Değişken Dönüşümü
- İki Eğri Arasında Kalan
- Alan Hesabı
- İntegral Uygulamaları:Dilimleme ve Bir Eksen Etrafında Döndürme ile Hacim Hesabı
- Silindirik
- Kabuklar Metodu ile Hacim Hesabı
- Düzlem Eğrilerin Uzunlukları
- Momentler ve Ağırlık Merkezi Hesabı
- Yüzey Alanları ve Pappus Teoremleri
- Transandantal Fonksiyonlar
- Doğal Logaritma
- Üstel Olarak Artma ve Azalma
- Üstel, Ters ve Trigonometrik Fonksiyonlar
- Hiperbolik Fonksiyonlar.
- İntegral Teknikleri:
- Kısmi İntegrasyon
- Rasyonel Fonksiyonların İntegrasyonu
- Trigonometrik
- İntegraller
- Trigonometrik Dönüşümler
- Sayısal İntegrasyon
- Genelleştirilmiş İntegraller.
- Konikler ve Kutupsal Koordinatlar:
- Konikler ve Kuadratik Denklemler
- Kutupsal Koordinatlar
- Kutupsal Koordinatlarda alan ve Yay Uzunluğu.
- Sonsuz Diziler ve Seriler:
- Diziler
- Sonsuz Seriler
- İntegral testi
- Karşılaştırma Testi
- Oran ve Kök Testi
- Alterne Seriler
- Kuvvet Serileri
- Taylor ve Maclaurin Serileri
- Fourier Serileri.
- Uzayda Vektörler: Vektörler
- Skaler ve Vektörel Çarpım
- Uzayda Doğru ve Düzlem Denklemleri
- Silindirler ve Kuadrik Yüzeyler.
- Vektör Değerli Fonksiyonlar:
- Vektör Değerli Fonksiyonların Limiti, Sürekliliği ve İntegrali
- Çok Değişkenli Fonksiyonlar:Limit
- Süreklilik
- Kısmi Türevler
- Doğrultuya Göre Türev
- Gradient Vektör
- Teğet
- Düzlem
- Normal Doğru Denklemi
- Lineerleştirme ve Diferansiyellenebilirlik
- Taylor Formülü
- İki ve Üç Katlı İntegraller
- Değişken
- Dönüşümleri ve Çok Katlı İntegrallerin Uygulamaları
- Çok Katlı Genelleştirilmiş İntegraller
- Eğrisel İntegraller
- Vektör Alanları
- Yoldan Bağımsızlık
- Potansiyel Fonksiyonu
- Eğrisel İntegrallerin Temel Teoremleri
- Düzlemde Green Teoremi
- Yüzey Alanı ve Yüzey İntegrali
- Stokes ve Diverjans teoremleri.
- Dizi Limitleri
- Sınırlı Diziler
- Gerçel Sayı Kümeleri
- Fonksiyonlarda Limit
- Sınırlı ve Monoton Fonksiyonlar
- Süreklilik
- Sürekli Fonksiyonların Özellikleri
- Düzgün Süreklilik
- İntegral Tanımı
- İntegralin Özellikleri
- Riemann İntegrallenebilirlik için Gerek ve Yeter Koşullar
- Noktasal ve Düzgün
- Yakınsaklık
- Kümeler ve Fonk.
- Diferansiyellenebilen Fonk.
- Kapalı ve Ters Fonk. Teoremleri
Özel Calculus Dersi ile İlgili Sıkça Sorulan Sorular ve Cevapları